Cited by
In this paper, we study the convergence rate of an Embedded exponential-type low-regularity integrator (ELRI) for the Korteweg-de Vries equation. We develop some new harmonic analysis techniques to handle the "stability" issue. In particular, we use a new stability estimate which allows us to avoid the use of the fractional Leibniz inequality,
and replace it by suitable inequalities without loss of regularity. Based on these techniques, we prove that the ELRI scheme proposed in [41] provides $\frac12$-order convergence accuracy in $H^\gamma$ for any initial data belonging to $H^\gamma$ with $\gamma >\frac32$, which does not require any additional derivative assumptions.
- BibTex
- RIS
- TXT
In this paper, we study the convergence rate of an Embedded exponential-type low-regularity integrator (ELRI) for the Korteweg-de Vries equation. We develop some new harmonic analysis techniques to handle the "stability" issue. In particular, we use a new stability estimate which allows us to avoid the use of the fractional Leibniz inequality,
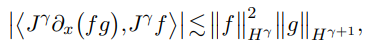
and replace it by suitable inequalities without loss of regularity. Based on these techniques, we prove that the ELRI scheme proposed in [41] provides $\frac12$-order convergence accuracy in $H^\gamma$ for any initial data belonging to $H^\gamma$ with $\gamma >\frac32$, which does not require any additional derivative assumptions.
}, issn = {}, doi = {https://doi.org/10.4208/aam.OA-2020-0001}, url = {http://global-sci.org/intro/article_detail/aam/18628.html} }In this paper, we study the convergence rate of an Embedded exponential-type low-regularity integrator (ELRI) for the Korteweg-de Vries equation. We develop some new harmonic analysis techniques to handle the "stability" issue. In particular, we use a new stability estimate which allows us to avoid the use of the fractional Leibniz inequality,
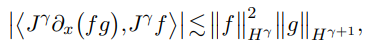
and replace it by suitable inequalities without loss of regularity. Based on these techniques, we prove that the ELRI scheme proposed in [41] provides $\frac12$-order convergence accuracy in $H^\gamma$ for any initial data belonging to $H^\gamma$ with $\gamma >\frac32$, which does not require any additional derivative assumptions.