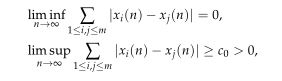In this paper, we propose a new method to study intermittent behaviors of coupled piecewise-expanding map lattices. We show that the successive transition between ordered and disordered phases occurs for almost every orbit when the coupling is small. That is,

where $x_i(n)$ correspond to the coordinates of $m$ nodes at the iterative step $n$. Moreover, when the uncoupled system is generated by the tent map and the lattice consists of two nodes, we prove a phase transition occurs between synchronization and intermittent behaviors. That is, $$\lim_{n\rightarrow \infty}| x_1(n)-x_2(n)|=0\quad\text{for }\ \ \Big|c-\frac12\Big|<\frac14$$ and intermittent behaviors occur for $|c-\frac12|>\frac14$, where $0\le c\le 1$ is the coupling.

We establish Hölder continuity of the horizontal gradient of weak solutions to quasi-linear $p$-Laplacian type non-homogeneous equations in the Heisenberg Group.

In this paper we study the initial boundary value problem for the system $\mbox{div}(\sigma(u)\nabla\varphi)=0,$ $ u_t-\Delta u=\sigma(u)|\nabla\varphi|^2$. This problem is known as the thermistor problem which models the electrical heating of conductors. Our assumptions on $\sigma(u)$ leave open the possibility that  $\liminf_{u\rightarrow\infty}\sigma(u)=0$, while $\limsup_{u\rightarrow\infty}\sigma(u)$ is large. This means that $\sigma(u)$ can oscillate wildly between $0$ and a large positive number as $u\rightarrow \infty$. Thus our degeneracy is fundamentally different from the one that is present in porous medium type of equations. We obtain a weak solution $(u, \varphi)$ with $|\nabla \varphi|, |\nabla u|\in L^\infty$ by first establishing a uniform upper bound for $e^{\varepsilon u}$ for some small $\varepsilon$. This leads to an inequality in $\nabla\varphi$, from which the regularity result follows. This approach enables us to avoid first proving the Hölder continuity of $\varphi$ in the space variables, which would have required that the elliptic coefficient $\sigma(u)$ be an $A_2$ weight.  As it is known, the latter implies that $\ln\sigma(u)$ is "nearly bounded''.

Başar and Braha [1], introduced the sequence spaces $\breve{\ell}_\infty$, $\breve{c}$ and $\breve{c}_0$ of Euler-Cesáro bounded, convergent and null difference sequences and studied their some properties. Then, in [2], we introduced the sequence spaces ${[\ell_\infty]}_{e.r}, {[c]}_{e.r}$ and ${[c_0]}_{e.r}$ of Euler-Riesz bounded, convergent and null difference sequences by using the composition of the Euler mean $E_1$ and Riesz mean $R_q$ with backward difference operator $\Delta$. The main purpose of this study is to introduce the sequence space ${[\ell_p]}_{e.r}$ of Euler-Riesz $p-$absolutely convergent series, where $1 \leq p <\infty$, difference sequences by using the composition of the Euler mean $E_1$ and Riesz mean $R_q$ with backward difference operator $\Delta$. Furthermore, the inclusion $\ell_p\subset{[\ell_p]}_{e.r}$ hold, the basis of the sequence space ${[\ell_p]}_{e.r}$ is constructed and  $\alpha-$, $\beta-$ and $\gamma-$duals of the space are determined. Finally, the classes of matrix transformations from the ${[\ell_p]}_{e.r}$ Euler-Riesz difference sequence space to the spaces $\ell_\infty, c$ and $c_0$ are characterized. We devote the final section of the paper to examine some geometric properties of the space ${[\ell_p]}_{e.r}$.

In this paper, we compare the mutual multifractal Rényi dimensions to the mutual multifractal Hausdorff and pre-packing dimensions. We also provide a relationship between the mutual multifractal Rényi dimensions of orthogonal projections of a couple of measures $(\mu,\nu)$ in $\mathbb{R}^n$. As an application, we study the mutual multifractal analysis of the projections of measures.