Cited by
- BibTex
- RIS
- TXT
Based on the Guo-Krasnoselskii's fixed-point theorem, the existence and
multiplicity of positive solutions to a boundary value problem (BVP) with two
integral boundary conditions
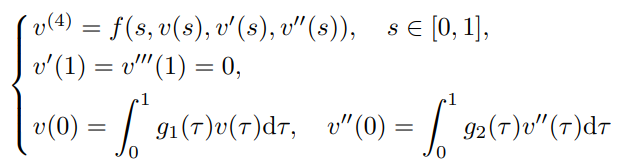
are obtained, where $f$, $g_1$, $g_2$ are all continuous. It generalizes the results of one positive solution to multiplicity and improves some results for integral BVPs. Moreover, some examples are also included to demonstrate our results as applications.
}, issn = {}, doi = {https://doi.org/}, url = {http://global-sci.org/intro/article_detail/aam/18585.html} }Based on the Guo-Krasnoselskii's fixed-point theorem, the existence and
multiplicity of positive solutions to a boundary value problem (BVP) with two
integral boundary conditions
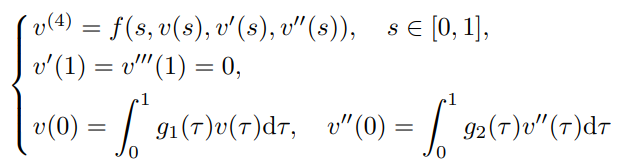
are obtained, where $f$, $g_1$, $g_2$ are all continuous. It generalizes the results of one positive solution to multiplicity and improves some results for integral BVPs. Moreover, some examples are also included to demonstrate our results as applications.
