Cited by
In this paper, the existence and multiplicity of positive solutions for a class
of non-resonant fourth-order integral boundary value problem
with two parameters are established by using the Guo-Krasnoselskii's fixed-point theorem, where $f∈C$([0,1]×[0,+∞)×(−∞,0], [0,+∞)), $q(t)∈L$1[0,1] is nonnegative, $α, β ∈ R$ and satisfy $β<2π$2, $α$>0, $α/π$4+$β/π$2<1, $λ$1,2=(−$β$∓$\sqrt{β^2+4α}$)/2. The corresponding examples are raised to demonstrate the results we obtained.
- BibTex
- RIS
- TXT
In this paper, the existence and multiplicity of positive solutions for a class
of non-resonant fourth-order integral boundary value problem
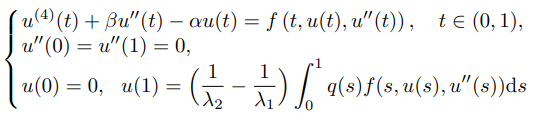
with two parameters are established by using the Guo-Krasnoselskii's fixed-point theorem, where $f∈C$([0,1]×[0,+∞)×(−∞,0], [0,+∞)), $q(t)∈L$1[0,1] is nonnegative, $α, β ∈ R$ and satisfy $β<2π$2, $α$>0, $α/π$4+$β/π$2<1, $λ$1,2=(−$β$∓$\sqrt{β^2+4α}$)/2. The corresponding examples are raised to demonstrate the results we obtained.
}, issn = {}, doi = {https://doi.org/}, url = {http://global-sci.org/intro/article_detail/aam/18087.html} }In this paper, the existence and multiplicity of positive solutions for a class
of non-resonant fourth-order integral boundary value problem
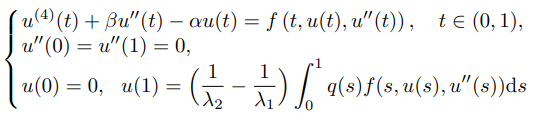
with two parameters are established by using the Guo-Krasnoselskii's fixed-point theorem, where $f∈C$([0,1]×[0,+∞)×(−∞,0], [0,+∞)), $q(t)∈L$1[0,1] is nonnegative, $α, β ∈ R$ and satisfy $β<2π$2, $α$>0, $α/π$4+$β/π$2<1, $λ$1,2=(−$β$∓$\sqrt{β^2+4α}$)/2. The corresponding examples are raised to demonstrate the results we obtained.