TY - JOUR
T1 - Asymptotic Stability for Gauss Methods for Neutral Delay Differential Equations
AU - Sidibe , Birama Sory
AU - Liu , Ming-Zhu
JO - Journal of Computational Mathematics
VL - 2
SP - 217
EP - 224
PY - 2002
DA - 2002/04
SN - 20
DO - http://doi.org/
UR - https://global-sci.org/intro/article_detail/jcm/8912.html
KW - Delay differential equations, Stability, Runge-Kutta methods.
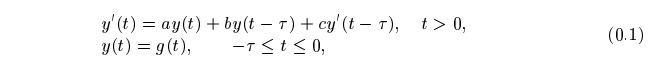
AB - <p style="text-align: justify;">In [4] we proved that all Gauss methods are $N \tau (0)$-compatible for neutral delay differential equations (NDDEs) of the form: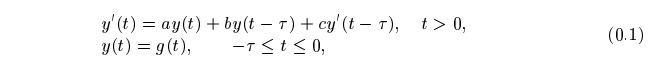<br/><img src="https://admin.global-sci.org/uploads/ueditor/image/20210803/1627962822498558.png" title="1627962822498558.png" alt="image.png"/><span style="text-align: center;"></span></p><p style="text-align: justify;">where $a, b, c$ are real, $\tau ＞0, g(t)$ is a continuous real valued function. In this paper we are going to use the theory of order stars to characterize the asymptotic stability properties of Gauss methods for NDDEs. And then proved that all Gauss methods are $N\tau(0)-$stable.<br/></p>