TY - JOUR
T1 - Fixed-Point Continuation Applied to Compressed Sensing: Implementation and Numerical Experiments
AU - Hale , Elaine T.
AU - Yin , Wotao
AU - Zhang , Yin
JO - Journal of Computational Mathematics
VL - 2
SP - 170
EP - 194
PY - 2010
DA - 2010/04
SN - 28
DO - http://doi.org/10.4208/jcm.2009.10-m1007
UR - https://global-sci.org/intro/article_detail/jcm/8514.html
KW - $\ell_1$ regularization, Fixed-point algorithm, Continuation, Compressed sensing,
Numerical experiments.
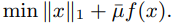
AB - <p style="text-align: justify;">Fixed-point continuation (FPC) is an approach, based on operator-splitting and continuation, for solving minimization problems with $\ell_1$-regularization:<br/> <br/></p><p style="text-align:center"><img src="https://admin.global-sci.org/uploads/ueditor/image/20210401/1617271753941055.png" title="1617271753941055.png" alt="image.png"/></p><p style="text-align: justify;"><br/>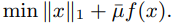We investigate the application of this algorithm to compressed sensing signal recovery, in which $f(x) = \frac{1}{2}\|Ax-b\|_M^2$, $A \in \mathbb{R}^{m \times n}$ and $m \leq n$. &nbsp;In particular, we extend the original algorithm to obtain better practical results, derive appropriate choices for $M$ and $\bar{\mu}$ under a given measurement model, and present numerical results for a variety of compressed sensing problems. The numerical results show that the performance of our algorithm compares favorably with that of several recently proposed algorithms.<br/></p>