TY - JOUR
T1 - The Nehari Manifold for a Class of Singular $\psi$-Riemann-Liouville Fractional with $p$-Laplacian Operator Differential Equations
AU - Horrigue , Samah
AU - Alsulami , Mona
AU - Alsaeedi , Bayan Abduallah
JO - Advances in Applied Mathematics and Mechanics
VL - 5
SP - 1104
EP - 1120
PY - 2024
DA - 2024/07
SN - 16
DO - http://doi.org/10.4208/aamm.OA-2022-0009
UR - https://global-sci.org/intro/article_detail/aamm/23287.html
KW - $\psi$-Riemann-Liouville fractional derivative, nonlinear fractional differential equations, $p$-Laplacian operator, existence of solutions, Nehari manifold method.
AB - <p style="text-align: justify;">Using Nehari manifold method combined with fibring maps, we show the
existence of nontrivial, weak, positive solutions of the nonlinear $\psi$-Riemann-Liouville
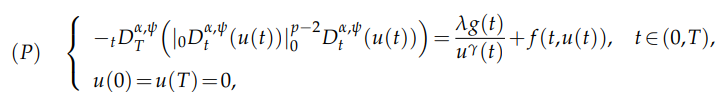
fractional boundary value problem involving the $p$-Laplacian operator, given by&nbsp;<br/></p><p style="text-align:center"><img src="https://admin.global-sci.org/uploads/ueditor/image/20240722/1721630403664206.png" title="1721630403664206.png" alt="image.png" width="514" height="64"/></p><p style="text-align: justify;">where $λ&gt;0, 0&lt;\gamma&lt;1&lt; p$ and $\frac{1}{p}&lt;\alpha≤1,$ $g∈C([0,T])$ and $f ∈C^1
([0,T]×\mathbb{R},\mathbb{R}).$ A useful
examples are presented in order to illustrate the validity of our main results.<br/></p>