TY - JOUR
T1 - Oscillation Theory of $h$-Fractional Difference Equations
AU - Li , Fanfan
AU - Han , Zhenlai
JO - Journal of Nonlinear Modeling and Analysis
VL - 1
SP - 105
EP - 113
PY - 2021
DA - 2021/04
SN - 3
DO - http://doi.org/10.12150/jnma.2021.105
UR - https://global-sci.org/intro/article_detail/jnma/18780.html
KW - $h$-deference equations, Oscillation, Fractional.
AB - <p style="text-align: justify;">In this paper, we initiate the oscillation theory for $h$-fractional
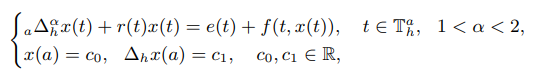
difference equations of the form<br/></p><p style="text-align:center"><img src="https://admin.global-sci.org/uploads/ueditor/image/20210506/1620268714544399.png" title="1620268714544399.png" alt="image.png"/></p><p style="text-align: justify;">where $_a∆^α_h$ is the Riemann-Liouville $h$-fractional difference of order $α$,&nbsp;$\mathbb{T}^a_h :$={$a + kh, k ∈&nbsp;\mathbb{Z}^+ $∪{0}}, and $a ≥ 0$, $h &gt; 0$. We study the oscillation of $h$-fractional difference equations with Riemann-Liouville derivative, and obtain
some sufficient conditions for oscillation of every solution. Finally, we give an
example to illustrate our main results.<br/></p>